[PLL] Phase Locked Loop, 위상 고정 루프, 선형·비선형 모델 비교, 위상각 점프와 주파수 변화

Phase locked loop linear/nonlinear model comparison (Phase Angle Jump, Frequency Change)

위상 고정 루프 선형·비선형 모델 비교(위상각 점프, 주파수 변화)

 

Part 1. Design Specifications, Theory and Formula Derivation(설계 사양, 이론 및 수식 유도)

Phase Locked Loop(PLL), 위상 고정 루프

: 신호 지연과 전송 중의 위상 변화로 인해 디지털 신호를 정확하게 수신하고 해석하는 것이 쉽지 않아 입력 신호가 어떻게 들어오던 간에 특정 위상점에서 들어오는 것처럼 고정한다.

• ★ 신호 지연과 위상 변화가 존재하더라도 정확한 신호해석이 가능하다.
• 주파수원이 흔들리지 않도록 고정해준다.
• 주파수원을 정확하게 가변한다.

위상 변화를 주었을 때 설정한 정착시간 내에 추적한다.

 

 

기본적인 PLL의 전달함수들이며 변수값을 임의로 설정하여 Plecs 상에서 구현하였다.

 

 

라플라스 변환을 이용한 소신호 모델에서의 전달함수이다.

 

 

뒷 내용부터는 Phase Angle Jump(위상각 점프)와 Frequency Modulation(주파수 변조)의 조건에서 어떤 동작을 하는지 Plecs로 구현한 로직과 실행한 스코프 화면을 보면서 비교해보도록 하겠습니다.

 

위상각 점프와 주파수 변조는 현실 세계에선 다 같은 noise(잡음)이기 때문에 두 가지가 따로따로 영향을 주진 않을 것입니다. 하지만 이와 같은 실험적인 부분에선 두가지를 함께 고려하면 계산도 복잡하고 어느 부분에서 오류가 있는지 찾기가 훨씬 더 어렵기 때문에 위상각 점프만 있는 조건, 주파수 변조만 있는 조건으로 각각 나누어 위상각 추적을 얼만큼 잘 하는가를 알아보도록 하겠습니다.

 

간단한 변수 조건들은 위 수식 사진에 있고 start time이 0.35초인 step함수를 통하여 위상각 점프와 주파수 변조를 하였습니다. 정착시간(Settling Time)은 0.1초로 설정하였습니다.

 

 

 

Part 2. Phase Angle Jump, Comparison of Linear Model and Nonlinear Model

선형 모델과 비선형 모델

 

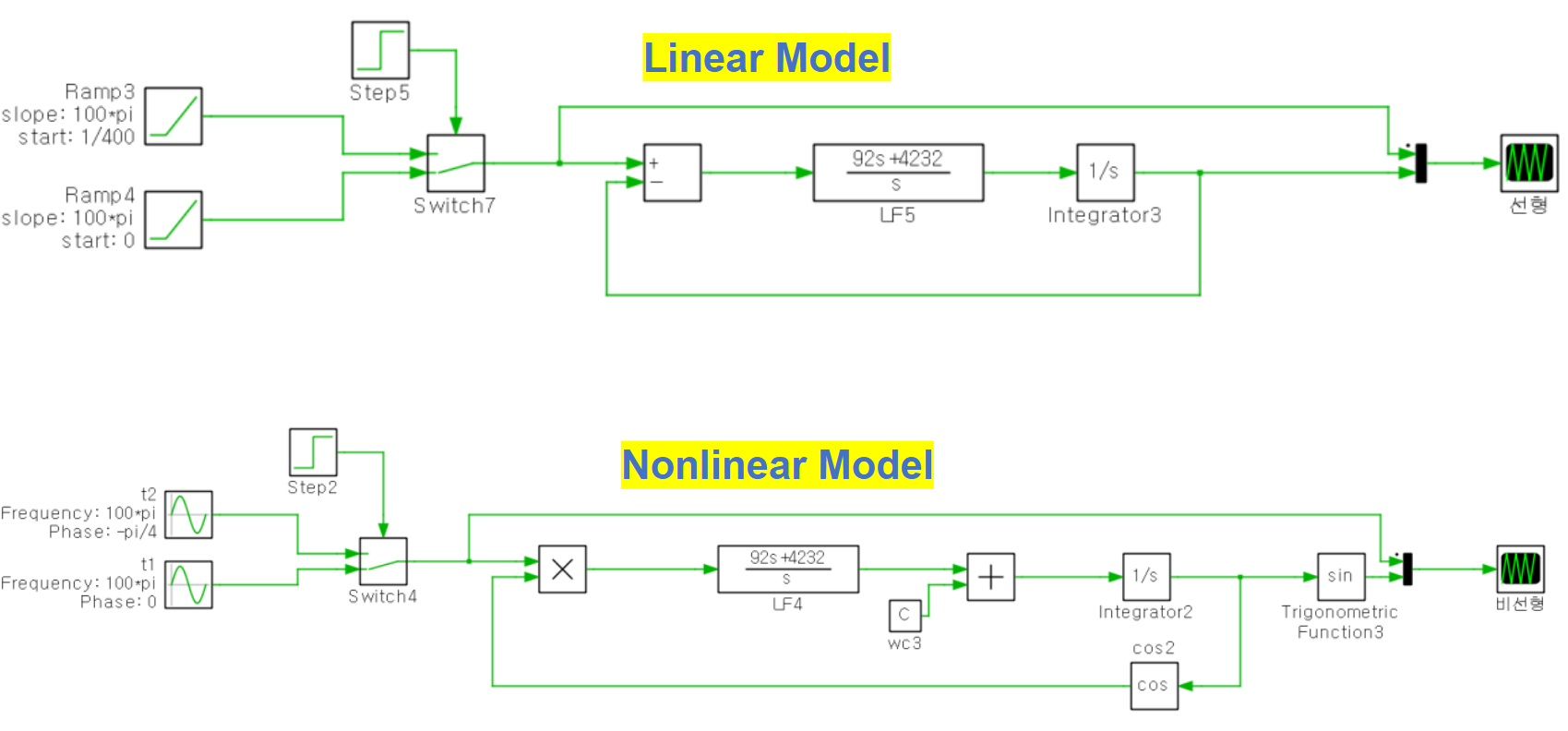
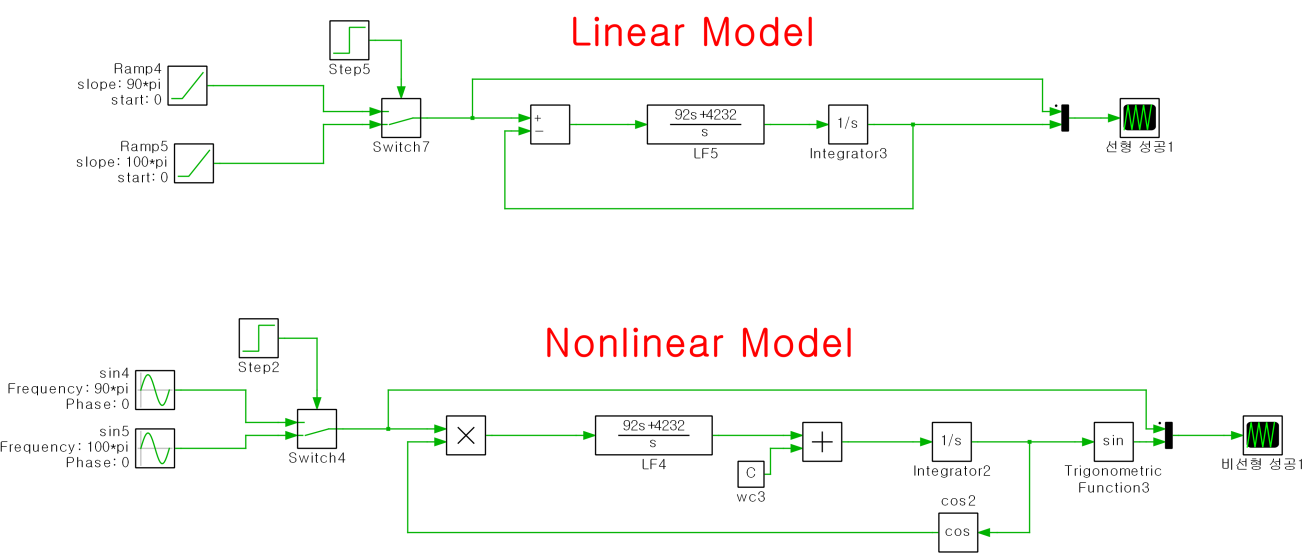
위 사진은 선형 모델과 비선형 모델의 위상각 점프를 Plecs 상에서 구현한 예시입니다.

입력 정현파와 램프 함수의 진폭은 1, 주파수는 50Hz로 주었습니다.

정현파 입력의 step 이후에 위상각 점프를 (- pi/4) 를 주었고 그에 맞게 step 이후의 램프 함수는 1/400초만큼 시작 시간을 늦추어주었습니다.

 

θ = 2*pi*f*t 공식을 이용하면 위상각과 시간 간의 변환을 쉽게 할 수 있습니다.

 

 

2-1. Linear Model의 뺄셈기 출력 & Nonlinear Model의 곱셈기 출력

 

Step Time Set : 0.35s ,  정상상태(Steady State) 진입 후에 위상각 변화를 주어야 하기 때문입니다.

English : To compare tracking by giving a phase angle jump after entering the steady state

파형 비교 사진

앞의 두 파형을 한 화면에서 비교한 사진이다.

 

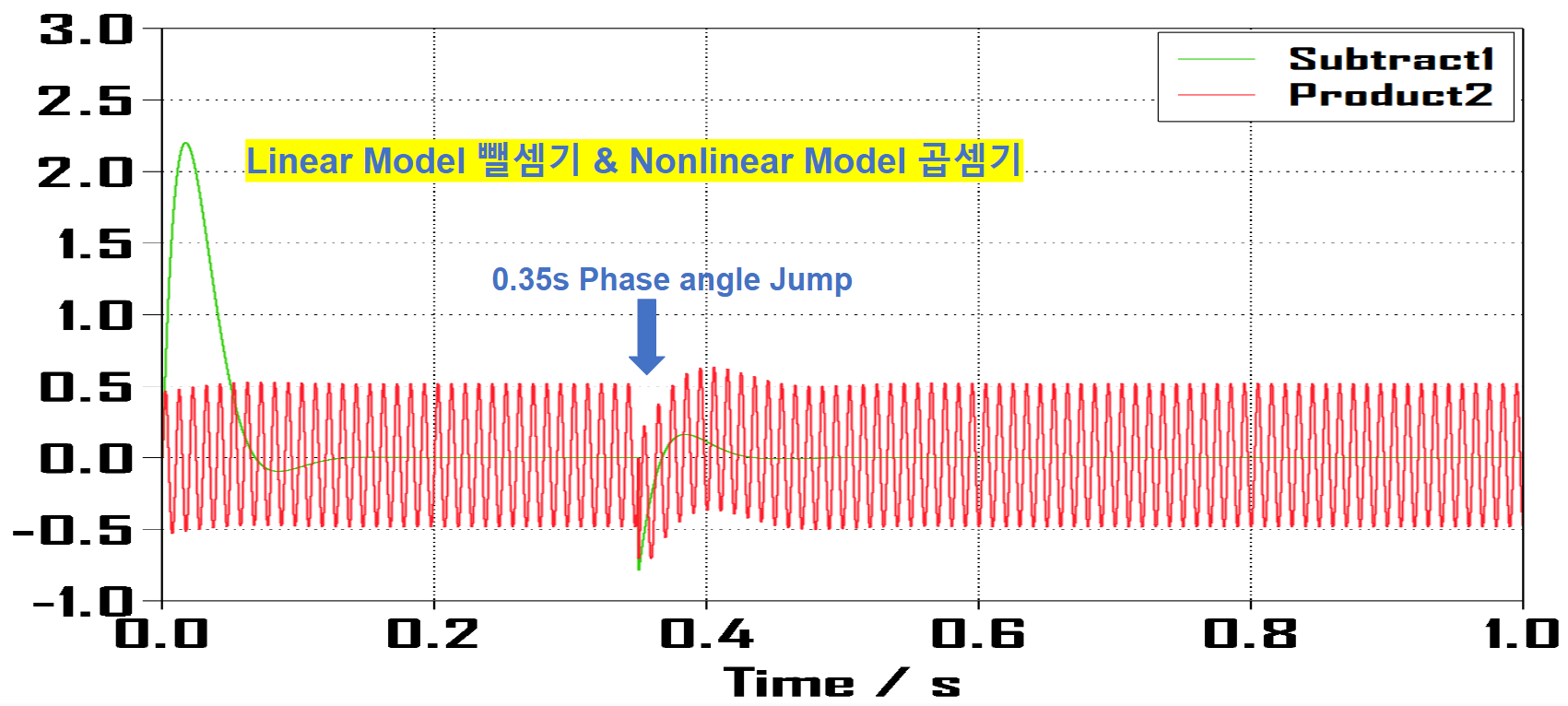
Linear Model의 뺄셈기와 Nonlinear Model의 곱셈기의 출력을 비교한 사진들 입니다.

즉 입력 신호와 궤환을 통해 들어온 신호를 비교기를 통해 전달함수가 입력 받는 파형인 것입니다.

선형 모델과 비선형 모델 모두 같은 파형을 지니고 있는 것을 알 수 있습니다.

 

 

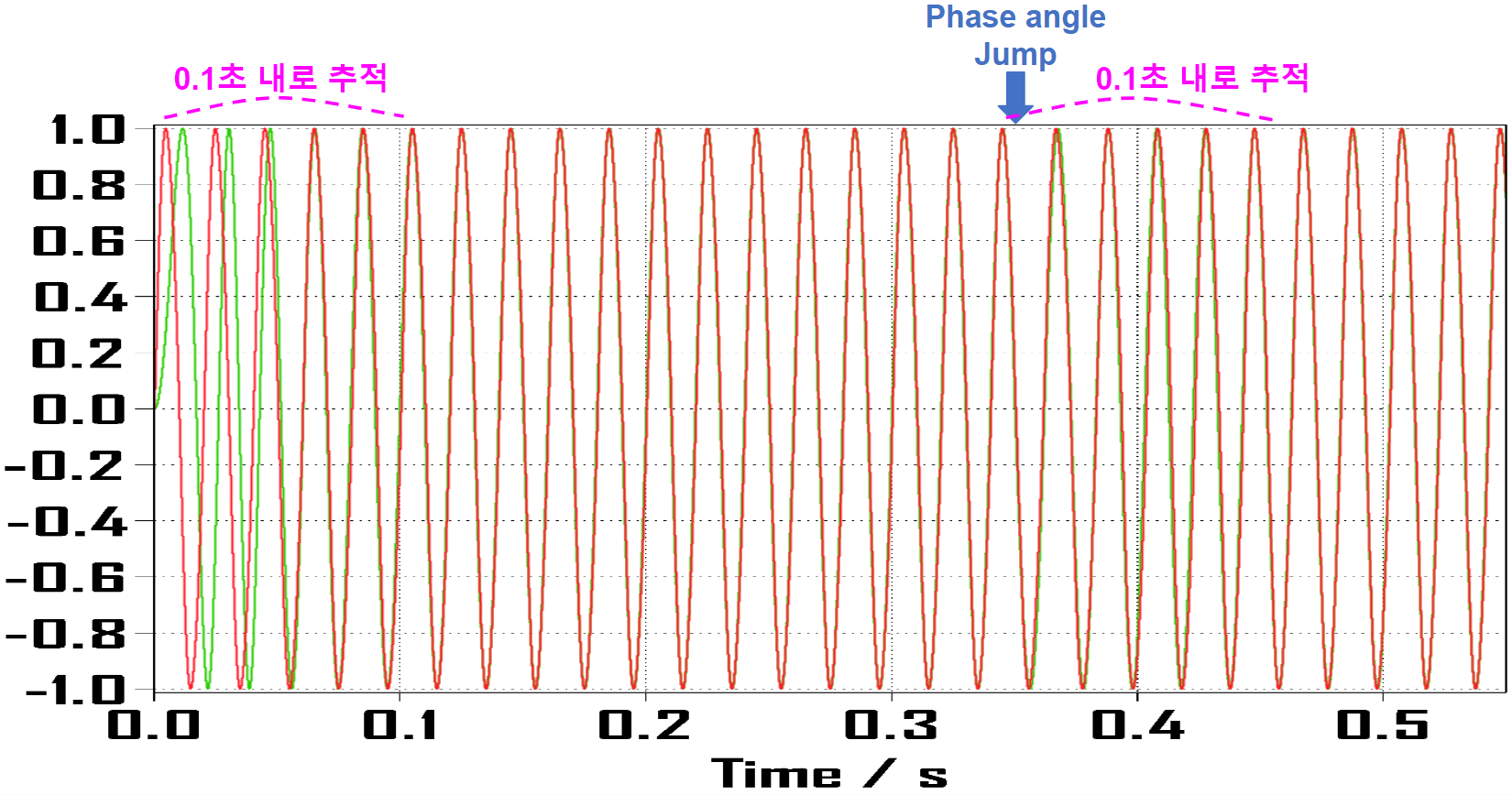
2-2. Linear Model의 최종 출력

정착시간(Settling Time) 0.1초 내로 추적함을 볼 수 있다.

시간대를 조금 더 나누어 확인하면 추적함을 확실히 알 수 있다.

 

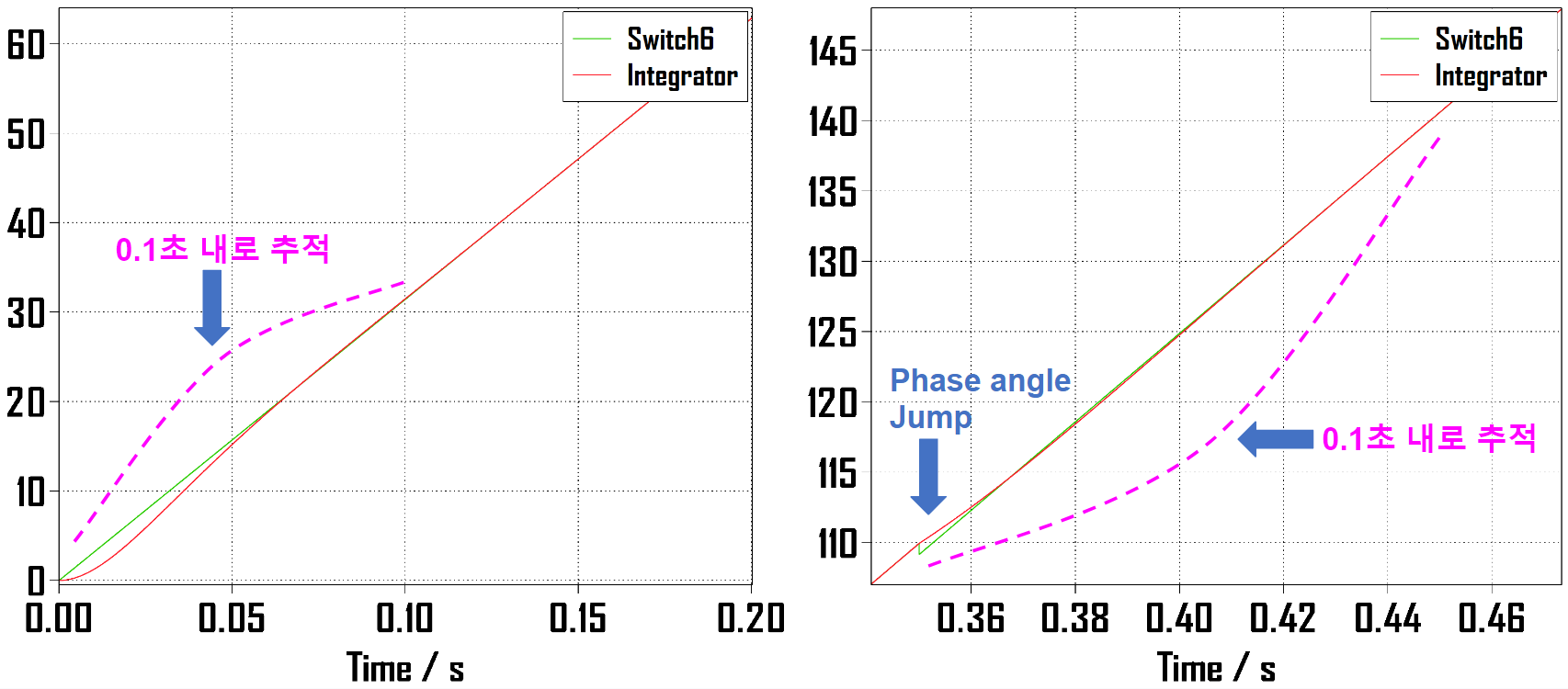
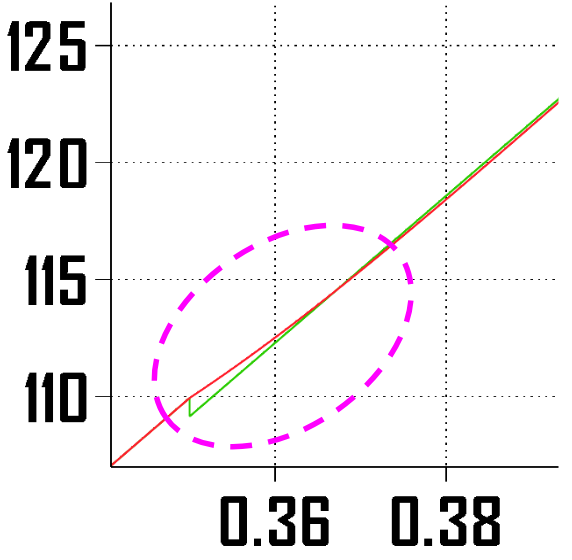
위상각 점프 pi/4에 맞게 시작시간을 1/400초만큼 늦춰주었기 때문에 origin(원점)에서부터 차이가 있고 정착시간인 0.1초 내로 추적함을 알 수 있습니다. 그리고 정상상태에 진입하여 진행하다가 0.35초에 위상각 점프를 하게 되면 두 그래프는 서로 어긋나게 되고 또다시 0.1초 내로 추적하여 거의 붙는 것을 볼 수 있습니다.

 

 

2-3. Nonlinear Model의 최종 출력

비선형 모델의 최종출력

 

위상각 점프 이후 파형 ZOOM IN

 

비선형 모델도 선형 모델과 마찬가지로 위상각 점프 이후 정착시간 0.1초 내에 다시 근접함을 볼 수 있습니다.

 

 

 

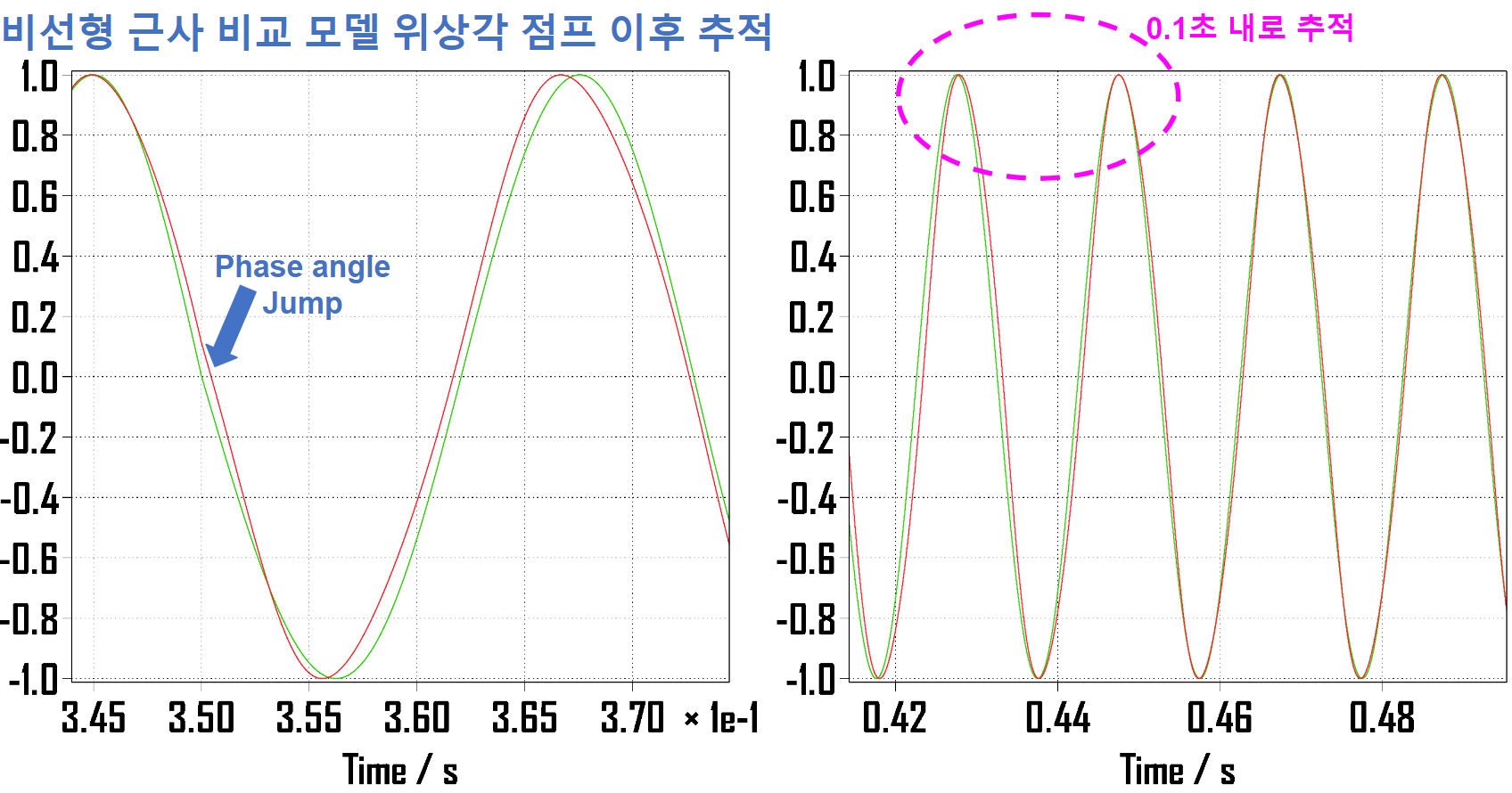
2-4. Linear Model vs Nonlinear Model(위상각 점프)

선형 모델과 비선형 모델의 출력을 선형과 비선형으로 근사하여 최종 확인

 

 

▶선형 근사 비교 모델

선형 근사 비교모델 스코프 실행 화면

선형 근사 비교모델 스코프 Zoom in

 

 

 

▶비선형 근사 비교 모델

비선형 근사 비교모델 스코프 실행 화면

비선형 근사 비교모델 스코프 Zoom in

비선형 근사 비교모델 위상각 점프 이후 Zoom in

 

 

 

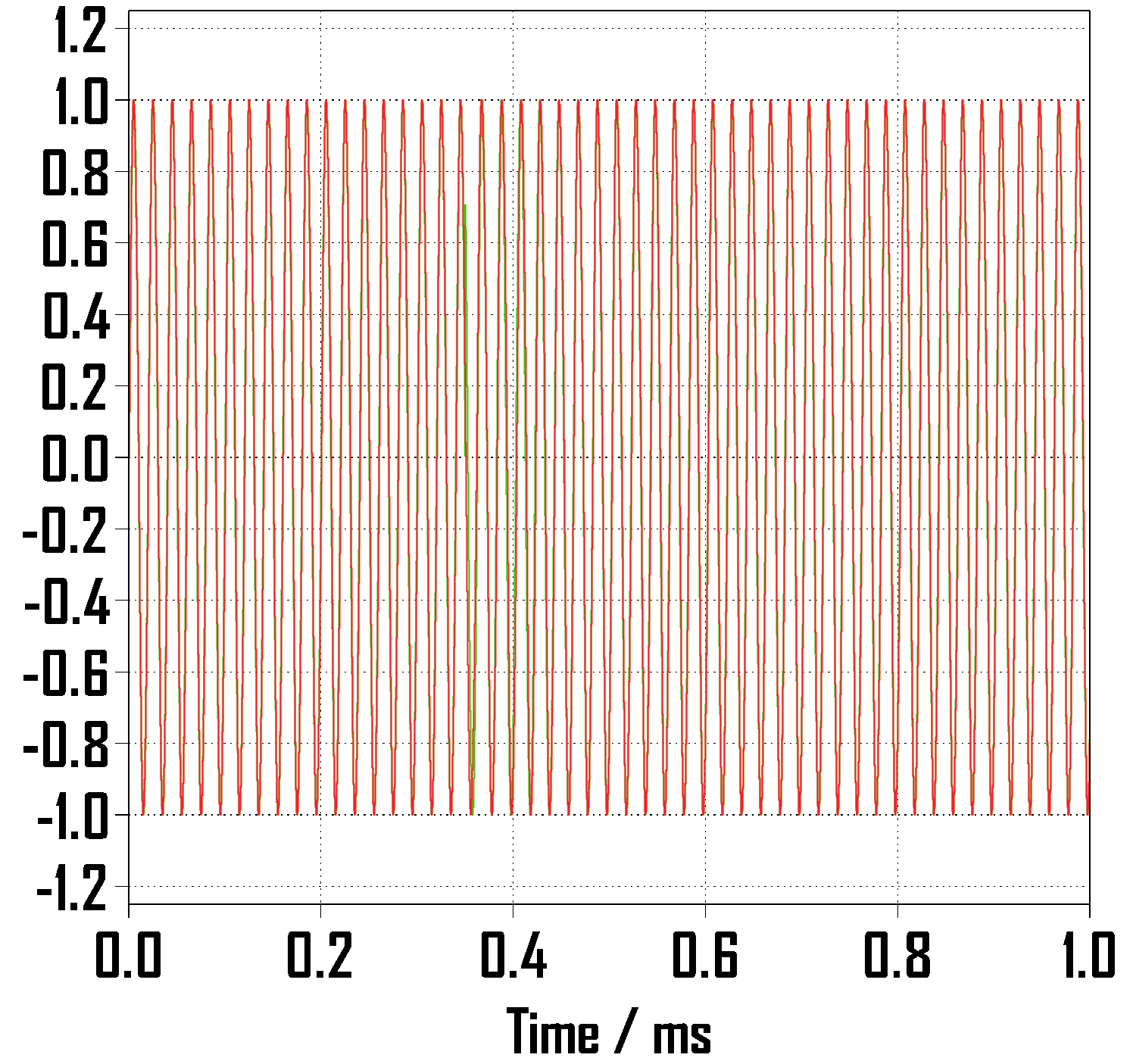
Part 3. Frequency Change, Comparison of Linear Model and Nonlinear Model

 

위 사진은 선형 모델과 비선형 모델의 주파수 변화를 Plecs 상에서 구현한 예시입니다.

입력 정현파와 램프 함수의 진폭은 1, 주파수는 50Hz→45Hz로 주었습니다.

 

입력 신호인 두 정현파와 두 램프함수가 같은지 확인하기 위해서 램프함수를 sin함수로 표현하여 비교해보았습니다.

완벽히 같은 것을 볼 수 있습니다.

 

이제 입력 신호가 모두 같은 신호라는 것도 확인이 되었으니 선형과 비선형 모델을 거쳐 최종 출력을 비교해보겠습니다.

 

 

3-1. Linear Model의 최종 출력

선형 모델의 최종 출력, 0.35초에 주파수가 바뀐 이후 다시 0.1초 내로 추적합니다.

주파수 바뀌는 부분 0.35초 이후 ZOOM IN

 

 

 

3-2. Nonlinear Model의 최종 출력

비선형 모델의 최종 출력, 0.35초에 주파수가 바뀐 이후 다시 0.1초 내로 추적합니다.

주파수가 바뀌는 부분 0.35초 이후 ZOOM IN

 

 

 

3-3. Linear Model vs Nonlinear Model(주파수 변화)

선형 모델과 비선형 모델의 출력을 선형과 비선형으로 근사하여 최종 확인

 

▶선형 근사 비교 모델

주파수 변화 선형 근사 비교

 

선형 근사 비교를 하였을 때 차이가 있는 것을 볼 수 있습니다. 하지만 기울기가 같으므로 같은 출력을 내고 있다는 것을 알 수 있습니다. 그러면 무엇 때문에 차이가 나느냐... 아래 사진을 통해 알아보겠습니다.

 

차이가 나는 이유

 

두 그래프의 차이를 비교해보면 (190.262 - 177.662 = 12.6)로 pi(=3.14)*4, 즉 4*pi 입니다.

2주기 정도의 차이가 있다는 이야기인데 이 부분에 대해서는 다음 포스팅에서 설명하도록 하겠습니다.

중요한 것은 선형과 비선형 두 모델이 같은 출력을 내고 있다는 것이고, 두 출력을 sin파로 바꾸어 비교하면 완전히 같을 것입니다. 이제 그 결과를 보도록 하겠습니다.

 

 

▶비선형 근사 비교 모델

주파수 변화 비선형 근사 비교

 

0.35초에 주파수가 변화하고 정착시간 내에 근접하는 것을 볼 수 있습니다. 시뮬레이션 성공이라는 것이죠.

주파수 변화 이후를 조금 더 자세히 볼까요.

주파수 변화 비선형 근사 비교, 주파수 변화 이후 ZOOM IN

 

주파수 변화 이후 서로 어긋났다가 0.45초 부근부터 다시 근접하는 것을 볼 수 있습니다.

 

 

 

지금까지 PLL, 위상고정루프에 대해서 Plecs 시뮬레이션을 통해 알아보았습니다.

기본적인 개념, 공식 및 수식 유도, 전달함수에 대한 것, Plecs 상에서 구현하는 법 등에 대해서 나름 꼼꼼하게 적었다고 생각합니다. 부족하거나 잘못된 부분이 있다면 댓글로 말씀해주시면 확인 후 곧바로 수정하겠습니다.

 

긴 글 읽어주셔서 감사합니다.